Melting of floating ice does not increase sea level. Or does it?

naturalheatengines

The level of water in a glass of water will usually increase as you drop an ice cube into it, but then will stay level as the ice cube melts. From this simple experiment easily done at home, it is usually inferred that the melting of floating ice should not contribute to increasing sea level.

At least, this is what I thought until I read a paper by [2]. This is when I realized that when an iceberg falls into the sea, it is only the volume of its submerged part that adds to the sea level increase, not its emerged part. As we all know, all icebergs have a tip that remains out of the water. When the iceberg melts, there must be an additional increase to sea level equals to the volume of its emerged part. Of course, we all know that the emerged fraction of an iceberg is small, which is what makes them so dangerous for navigation, think Titanic, but how small? What is the physics determining the volume of the emerged part of an iceberg?

The celebrated Archimedes principle is the key to the answer. Physically, Archimedes principle states that the floating iceberg experiences an upward force equals to the volume of seawater that it displaced. Mathematically:

F_{archimedes} = \rho_{sw} V_{in} g,

where \rho_{sw} is the density of seawater, V_{in} is the volume of the submerged part of the iceberg, and g is the acceleration of gravity. Now, the floating iceberg also experiences a downward force due to its own weight,

{\Large F_{gravity} = m_{ice} g = V_{ice} \rho_{ice} g},

where V_{ice} and m_{ice} are the total volume and mass of the iceberg respectively, and \rho_{ice} the density of ice.

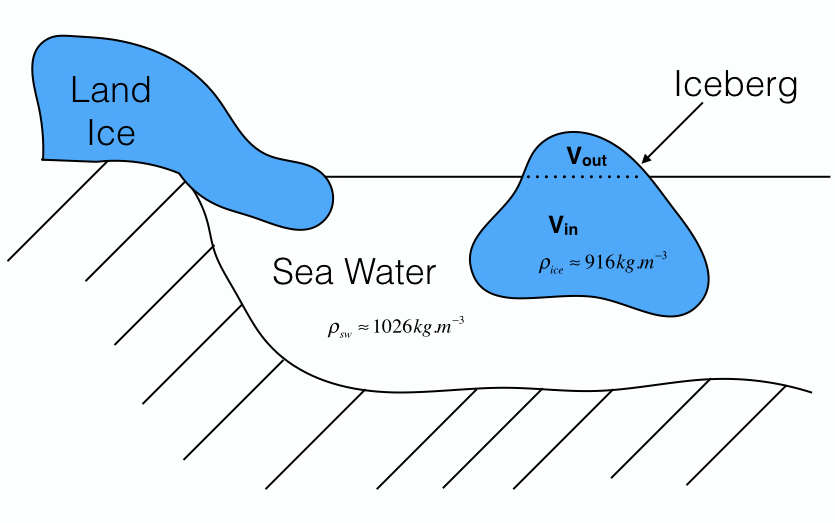
blog2_iceberg
Fig. 1: Schematics illustrating the effect of dumping land ice into the ocean. Initially, sea level coincides with z=0, and has slightly increased following the addition of the iceberg.

Now, if we equate the two forces, which must be the case for an iceberg at equilibrium, we get the following equation:

V_{in} = (\rho_{ice}/\rho_{sw}) V_{ice}

which demonstrates that floating icebergs can never be totally submerged because the density of ice \rho_{ice}\approx 916\,{\rm kg.m^{-3}} is always much smaller than the density of seawater \rho_{sw}\approx 1026\,{\rm kg.m^{-3}}. Now, to estimate the level increase \Delta h_{ice} due to the floating iceberg, one needs to equate the submerged iceberg volume V_{in} with the corresponding volume of seawater displaced, that is, A_{ocean} \Delta h_{ice}, where A_{ocean} is the area of the ocean. Reorganizing yields the following expression for \Delta h_{ice}:

\Delta h_{ice} = \frac{V_{in}}{A_{ocean}} = \frac{\rho_{ice}}{\rho_{sw}} \frac{V_{ice}}{A_{ocean}}

Now, in order to estimate the total sea level increase \Delta h_{melt} that would have resulted from first melting the iceberg before dumping it into the ocean, one can simply use the fact that the mass of the iceberg is the same in its frozen (volume V_{ice} and density \rho_{ice})) and melted (volume V_f and density \rho_f) forms. Mathematically, \rho_{ice} V_{ice} = \rho_{f} V_{f}, which implies V_f = (\rho_{ice}/\rho_f)V_{ice}. This states that the volume of the iceberg once melted is less than the volume it had when frozen, consistent with the well known result that ice is less dense than freshwater. Freshwater expands as it freezes, unlike most other fluids. As a result, the sea level increase due to a completely melted iceberg is therefore equal to:

\Delta h_{melt} = \frac{\rho_{ice}}{\rho_f} \frac{V_{ice}}{A_{ocean}}

Now, we can compute the difference between the sea level increase due to a completely melted iceberg minus that of a frozen iceberg:

\Delta h_{melt} - \Delta h_{ice} = \frac{\rho_{ice}(\rho_{sw}-\rho_f)}{\rho_{sw} \rho_f}\frac{V_{ice}}{V_{ocean}} = \frac{\rho_{sw}-\rho_f}{\rho_f} \Delta h_{ice}

This result shows that the ultimate cause for the additional sea level increase due to the melting of floating ice is the difference in density between fresh and seawater. In other words, melting ice cubes in a glass of freshwater would not result in any additional volume increase, as per conventional wisdom. The effect is quite small. For \Delta h_{ice} = 1 m, the additional increase would be (1026-1000)/1000 \times \Delta h_{ice} = 2.6 cm. This small effect is nevertheless comparable to the level of remaining uncertainties in closing the sea level budget.

In the above discussion, the temperature and salinity are assumed to remain constant. [1] argue, however, that melting the floating ice requires energy that must come primarily from the ocean. The resulting cooling would contract, and act to some extent to negate the effect. Arguably, volume changes due to temperature changes must be treated separately, as they belong to the contraction/expansion effect. Moreover, mixing freshwater with salty water will also result in some contraction.

REFERENCES

[1] Jenkins A. and D. Holland, 2007. Melting of floating ice and sea level rise. Geophys. Res. Lett, 34, L16609, doi:10.1029/2007GL030784
[2] Noerdlinger, P. D. and K. R. Brower, 2007. The melting of floating ice raises the ocean level. Geophys. J. Int., 170, 145-150.

PHOTO CREDITS

[a] Picture of iceberg from Wiki Commons.

[b] Schematics. Author: Remi Tailleux Licence CC-BY

Unknown's avatar

Published by naturalheatengines

Leave a comment